Build a Scorecard • KAscore

Once you have decided on a final set of features (i.e., independent variables), you are ready to build a scorecard model.

Fit a Logistic Regression Model

While it is possible to leverage other algorithms when creating a scorecard model, the traditional approach is to use logistic regression. In a future release of this package, we will document how to create a scorecard using a different model type. But for now, let’s fit a logistic regression model between our dependent variable default_status and our new WoE independent variables:

# Reverse levels of `default_status`; see ?woe "Details" section
loans$default_status <- factor(loans$default_status, levels = c("good", "bad"))

# Pre-process the data to create WoE features
train <- woe(
  data = loans,
  outcome = default_status,
  predictors = c(industry, housing_status),
  method = "replace",
  verbose = FALSE
)

# Fit the logistic regression model
fit <- glm(
  formula = default_status ~  ., 
  data = train, 
  family = "binomial"
)

summary(fit)
#> 
#> Call:
#> glm(formula = default_status ~ ., family = "binomial", data = train)
#> 
#> Coefficients:
#>                    Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)        -0.84592    0.07115 -11.889  < 2e-16 ***
#> woe_industry       -0.99115    0.17648  -5.616 1.95e-08 ***
#> woe_housing_status -0.99867    0.24140  -4.137 3.52e-05 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 1221.7  on 999  degrees of freedom
#> Residual deviance: 1170.3  on 997  degrees of freedom
#> AIC: 1176.3
#> 
#> Number of Fisher Scoring iterations: 4

In interpreting the coefficients above, we must remember that having “bad” as the second (i.e., target) level in our logistic regression model means that we are trying to predict the probability of “bad” (as opposed to the probability of a loan being “good”). With this in mind, note that the coefficients of our model above are negative. This means that at the time of scoring a new loan, higher (and positive) input WoE values will decrease the value returned by the model (i.e., decrease the probability that the observation is “bad”), while lower (and negative) input WoE would return a higher predicted probability of “bad”.

If we recall that higher (positive) WoE values mean that there is a greater proportion of “goods” than “bads”, and lower (negative WoE) values mean that there is a greater proportion of “bads” than “goods”, we would expect a dataset that generally has more “good” observations than “bad” observations to produce a fitted glm model that has mostly negative coefficients.

Note: In this simplified example, we used the entire loans dataset to train the logistic regression model. In practice, you will want to split your data into “train” and “test” sets for the purposes of assessing model accuracy.

Determining Target Points & Target Odds

After fitting the logistic regression model, there are three important decisions that must be made when converting it into a scorecard:

What is the “target” number of points?
What are the odds (good:bad) at the target number of points?
What are \(x\) and \(y\) such that the odds (good:bad) increase by a factor of \(x\) every \(y\) points?

While the first and second decisions in the list above are relatively straightforward, the odds() function may help with determining what those \(x\) (the odds growth factor, referred to as pxo) and \(y\) (the number of points to increase the score by relative to the growth factor, referred to as the rate) values should be.

Take the following example. Let’s suppose we want to build a scorecard where a score of 600 has odds of 30:1 (i.e., for every 31 loans that score a 600, we expect 30 to be good loans and 1 loan to be bad).

target_points <- 600
target_odds <- 30

How should the odds change for scores above and below 600? Let’s say that every 50 points, the odds double:

growth_points <- 50
growth_rate <- 2   # 2 == "double the odds", 3 == "triple the odds", etc.

Let’s simulate a bunch of different possible scores:

(scores <- seq.int(500, 700, 25))
#> [1] 500 525 550 575 600 625 650 675 700

Lastly, let’s get the odds associated with each score simulated above:

odds_by_score <- odds(
  score = scores, 
  tgt_points = target_points, 
  tgt_odds = target_odds, 
  pxo = growth_points, 
  rate = growth_rate
)

tibble::tibble(
  score = scores,
  odds = odds_by_score |> round(2)
)
#> # A tibble: 9 × 2
#>   score  odds
#>   <dbl> <dbl>
#> 1   500   7.5
#> 2   525  10.6
#> 3   550  15  
#> 4   575  21.2
#> 5   600  30  
#> 6   625  42.4
#> 7   650  60  
#> 8   675  84.8
#> 9   700 120

It may help to instead plot the data in the table above (i.e., the relationship between scores and associated odds) for easier interpretation.

plot(
  x = scores,
  y = odds_by_score,
  type = "b",
  xlab = "Score",
  ylab = "Odds (bad:good, reduced to y:1)", 
  ylim = c(0, 125), 
  main = "Odds by Score"
)

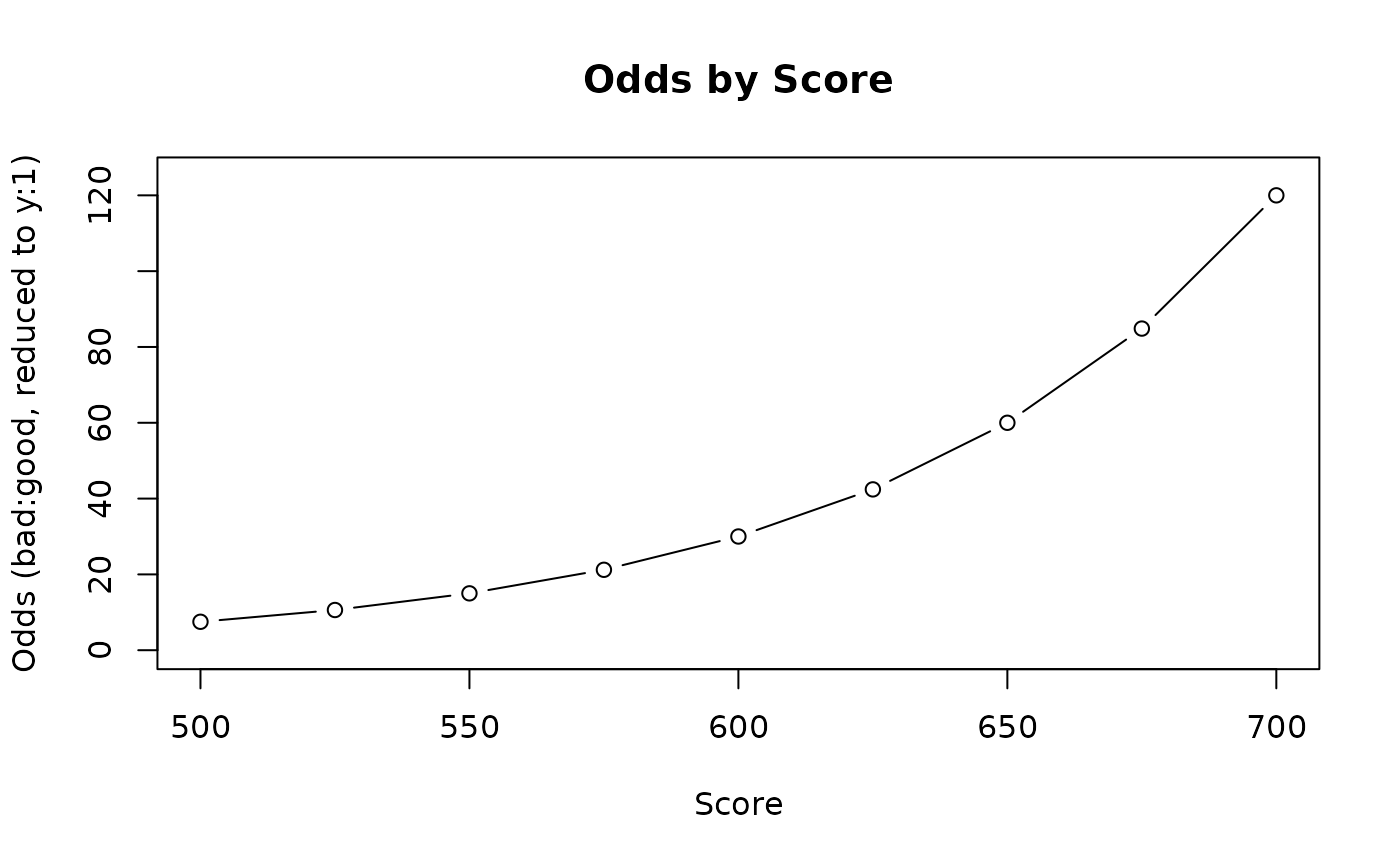
From both the table and the plot, we can see that the function correctly returned 30:1 odds at a score of 600 (our target specifications). Further, the odds are doubled (60:1) at a score of 650 and again at 700 (120:1), and halved (15:1) at a value of 550 and again at 500 (7.5:1). This lines up precisely with the values we set for the pxo and rate arguments.

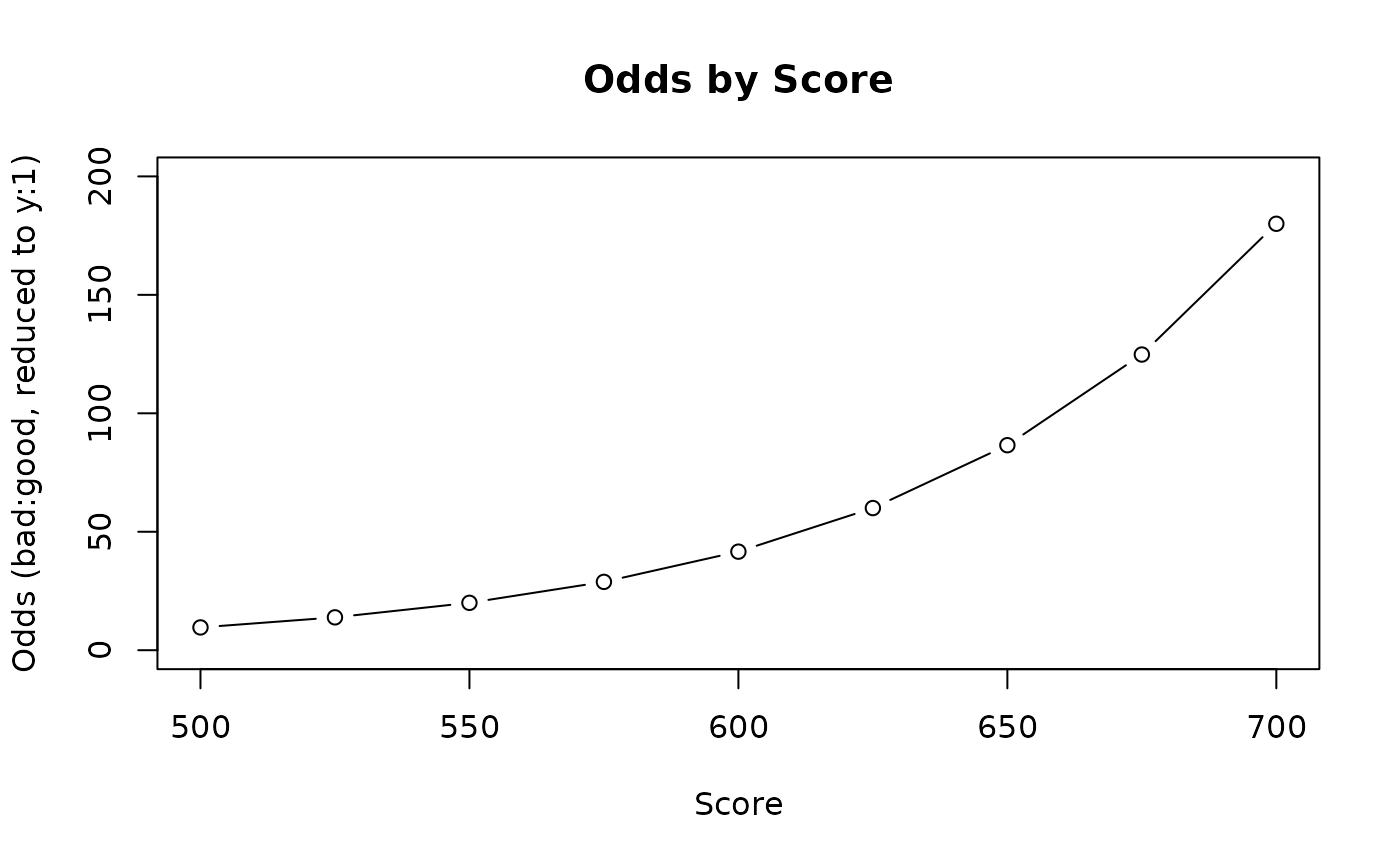
We can continue to try changing the odds() parameters and seeing how the odds respond to the input points, until we have a relationship that we are comfortable with using in our scorecard:

# A score of 550 has 20:1 odds, and the odds triple every 75 points
odds_by_score_new <- odds(
  score = scores, 
  tgt_points = 550,
  tgt_odds = 20,
  pxo = 75, 
  rate = 3
)

plot(
  x = scores,
  y = odds_by_score_new,
  type = "b",
  xlab = "Score",
  ylab = "Odds (bad:good, reduced to y:1)", 
  ylim = c(0, 200),
  main = "Odds by Score"
)

Map Scorecard Points

Finally, we can combine our logistic regression model with the target points, target odds, growth rate, and number of points to increase the odds (at that growth rate) to map the logit model intercept and coefficients to a number of points. This package offers a convenient points() function to help you do this:

# Extract the model's parameter estimates & intercept
params <- fit$coefficients |>
  tibble::as_tibble(rownames = NA) |>
  tibble::rownames_to_column(var = "variable")

# Build the scorecard base dictionary
dict <- woe(
  data = loans,
  outcome = default_status,
  predictors = c(industry, housing_status),
  method = "dict",
  verbose = FALSE
) |>
  dplyr::transmute(
    variable = paste0("woe_", variable),
    class = class,
    woe = woe
  ) |>
  dplyr::inner_join(params, by = "variable")

# Specify the target points/odds and growth parameters:
#   A score of 300 points has odds of 30:1 (good:bad), and the odds double every 
#   20 points
card_points <- 300
card_odds <- 30
card_pxo <- 20
card_rate <- 2

# Add the points, creating the final scorecard
card <- dict |>
  dplyr::mutate(
    points = points(
      woe = woe,
      estimate = value,
      intercept = params$value[params$variable == "(Intercept)"],
      num_vars = length(params$variable[params$variable != "(Intercept)"]),
      tgt_points = card_points,
      tgt_odds = card_odds,
      pxo = card_pxo,
      rate = card_rate
    )
  )

card
#> # A tibble: 12 × 5
#>    variable           class            woe  value points
#>    <chr>              <chr>          <dbl>  <dbl>  <dbl>
#>  1 woe_industry       ""            1.23   -0.991    148
#>  2 woe_industry       "beef"       -0.231  -0.991    107
#>  3 woe_industry       "dairy"      -0.0956 -0.991    110
#>  4 woe_industry       "fruit"      -0.359  -0.991    103
#>  5 woe_industry       "grain"       0.410  -0.991    125
#>  6 woe_industry       "greenhouse" -0.511  -0.991     99
#>  7 woe_industry       "nuts"       -0.288  -0.991    105
#>  8 woe_industry       "pork"       -0.606  -0.991     96
#>  9 woe_industry       "poultry"     0.774  -0.991    135
#> 10 woe_industry       "sod"        -0.154  -0.991    109
#> 11 woe_housing_status "own"         0.194  -0.999    119
#> 12 woe_housing_status "rent"       -0.430  -0.999    101

To hand this card off to others, it may be easier to simplify to just the variable, class, and points:

card_clean <- card |> 
  dplyr::mutate(
    variable = gsub(pattern = "woe_", replacement = "", x = variable)
  ) |> 
  dplyr::select(-value)

card_clean |> 
  knitr::kable()

variable	class	woe	points
industry		1.2321428	148
industry	beef	-0.2305237	107
industry	dairy	-0.0955565	110
industry	fruit	-0.3592005	103
industry	grain	0.4100628	125
industry	greenhouse	-0.5108257	99
industry	nuts	-0.2876821	105
industry	pork	-0.6061358	96
industry	poultry	0.7738360	135
industry	sod	-0.1541508	109
housing_status	own	0.1941560	119
housing_status	rent	-0.4302047	101

Note that the scorecard() function (demonstrated below) also expects a “clean” version of the card supplied to its card argument. While this may seem counter-intuitive given that the values in the variable column (of the data frame passed to the card argument) will not match the names of the independent variables in the glm object (passed to the fit argument, which should all start with “woe_”), we have found that users are almost always working with a “clean” version of the card in their downstream workflows, and it can be confusing to manage multiple versions of the same scorecard.

Building a Scorecard Model Object

The scorecard() function enables users to create a model object against which predict() can be called. scorecard() expects two arguments representing:

the glm model object (whose independent variables should be prefixed by “woe_”), and
the “clean” version of the scorecard (i.e., the independent variables should be named identically in each object passed to scorecard()).

scorecard_fit <- scorecard(
  fit = fit,
  card = card_clean
)

# You can view a model summary with a call to  `summary()`
# summary(scorecard_fit)

Scoring a New Loan

To score a new loan, let’s pretend that we have a loan with the following data:

Industry = grain
Housing Status = own

# Create a data frame containing the new loan's data
new_data <- tibble::tribble(
  ~industry, ~housing_status, 
  "poultry", "own"
)

new_data |> 
  knitr::kable()

industry	housing_status
poultry	own

We can call predict() against our new scorecard_fit object, passing in the new_data to be scored.

new_loan_points <- predict(
  object = scorecard_fit,
  newdata = new_data,
  type = "points"
)

paste0("New Loan Score: ", new_loan_points)
#> [1] "New Loan Score: 254"

Note that the type argument can be either "points" or "prob" (will default to "points" if not specified). Specifying type = "prob" will return the glm class probability (i.e., the probability of being a “bad” loan).

new_loan_prob <- predict(
  object = scorecard_fit,
  newdata = new_data,
  type = "prob"
)

paste0("New Loan Probability of 'Bad': ", scales::percent(new_loan_prob))
#> [1] "New Loan Probability of 'Bad': 14%"