Ongoing Monitoring • KAscore

As with any model that is in production, it’s important to continuously monitor a scorecard model’s performance to ensure its robustness and ability to separate a “good” loan from a “bad” loan.

This vignette details how to perform the following monitoring exercises:

Create Score Range Bins for Assessing Population Stability
Calculate the Population Stability Index
Calculate the Chi-Squared Goodness of Fit Test
Calculate the Characteristic Analysis Index
Compare Multiple Monitoring Time Horizon Windows

The vignette concludes with additional considerations for utilizing domain experts, monitoring variables not currently in the production model, and what to do when your monitoring processes indicate that your production model is weakening.

Similar to the {KAscore} package itself, the content herein is largely based upon the book Intelligent Credit Scoring: Building and Implementing Better Credit Risk Scorecards by Naeem Siddiqi (2nd Edition).

Terminology

Throughout this vignette, we will refer to the “development” sample and the “monitoring” sample.

The development sample is the data that was used to develop the scorecard model that is currently in production.

The monitoring sample is the new data that has been scored by the model since it was put into production.

Population Stability

The population stability index compares the sample distributions between the development data and the monitoring data across score ranges.

Said another way, this index compares the proportion of loans in the development data that scored (for example) between 200-210 with the proportion of loans in the monitoring sample that scored between 200-210; then compares the proportion of loans in the development data that scored (for example) between 211-220 with the proportion of loans in the monitoring sample that scored between 211-220; and so on. This index helps answer the question: “Does our recent applicant pool continue to look like the applicant pool that the model was trained on?”

There are multiple ways to specify the score ranges necessary to develop the population stability index, including:

Set score ranges such that you end up with an equal number of development sample cases in each bin; the bin_quantile() function from {KAscore} can automatically compute equally sized range bins
Set uniform score ranges that are (for example) 20 points apart; i.e., (300, 320], (320, 340], etc; his approach can provide “cleaner” cutoff values within the ranges, but may result in some bins that have very few development sample cases
Define custom score ranges that are perhaps the result of a hybrid approach between the two methodologies above (e.g., adjust the quantile bins slightly so that the range cutoffs to have “cleaner” breaks)

Developing Score Range Bins

Suppose we used the woe(), glm(), and points() functions (as described in Build a Scorecard) to create the following scorecard that is being used in production:

Scorecard in Production
Variable	Class	Points
industry		110
industry	beef	69
industry	dairy	73
industry	fruit	65
industry	grain	87
industry	greenhouse	61
industry	nuts	67
industry	pork	58
industry	poultry	97
industry	sod	71
housing_status	own	79
housing_status	rent	67
collateral_type	building society savings agreement/ life insurance	75
collateral_type	car or other, not in attribute Savings account/bonds	75
collateral_type	real estate	85
collateral_type	unknown / no property	63

Now suppose this card has been in production for a month, and 200 new loans have been scored using the model. We can view the first few loans in this monitoring sample in the table below:

Monitoring Sample
Loan ID	Industry	Housing Status	Collateral Type	Points Scored
500001	fruit	own	building society savings agreement/ life insurance	219
500002	dairy	rent	real estate	225
500003	grain	rent	car or other, not in attribute Savings account/bonds	229
500004	poultry	own	car or other, not in attribute Savings account/bonds	251
500005	grain	rent	building society savings agreement/ life insurance	229
500006	grain	rent	car or other, not in attribute Savings account/bonds	229

From a monitoring perspective, we want to compute the population stability index to ensure that the data scored by the model in the last month aligns with the data used to develop the model.

First, we will need to assign points to our development sample (the number of points each applicant in the development sample would have scored if the model was in production).

Development Sample
Loan ID	Industry	Housing Status	Collateral Type	Points Scored
100100	grain	own	real estate	251
100101	grain	own	real estate	251
100102	pork	own	real estate	222
100103	dairy	rent	building society savings agreement/ life insurance	215
100104	fruit	rent	unknown / no property	195
100105	pork	rent	unknown / no property	188

Next, we have to create score range bins using the scores our development sample data would have received. The bin_quantile() function from {KAscore} may provide a good starting point.

# Create six score range bins using the scores from the development sample
development_sample <- development_sample |> 
  dplyr::mutate(
    bin = bin_quantile(
      points, 
      n_bins = 6L,
      min_value = min(points),
      max_value = max(points),
    )
  )

# Show score range bins & proportion of the development sample in each of them
development_score_ranges <- development_sample |> 
  dplyr::count(bin) |> 
  dplyr::mutate(prop = n / sum(n))

development_score_ranges |> 
  dplyr::mutate(prop = scales::percent(prop)) |> 
  knitr::kable(
    col.names = c(
      "Score Range", 
      "# of Cases in Development Sample", 
      "% of Development Sample"
    ), 
    align = c("l", "r", "r"),
    caption = "Score Range Bins (Using Development Sample)"
  )

Score Range Bins (Using Development Sample)
Score Range	# of Cases in Development Sample	% of Development Sample
[188,215]	192	19.2%
(215,221]	142	14.2%
(221,227]	194	19.4%
(227,237]	153	15.3%
(237,241]	166	16.6%
(241,274]	153	15.3%

Note that even when performing quantile binning or manual binning, it may be difficult to achieve a perfectly equal proportion of the data across all score range bins, depending on your scorecard. By definition, scorecards have a finite number of possible of points that an applicant can receive, based upon the different combinations of the loan applicant attributes (i.e., the classes within each independent variable). For scorecards with fewer independent variables (and/or few classes within the independent variables), this can result in large proportions of the development sample data that have the exact same score. Because we are binning integers, this can result in bins that are not perfectly equal in size.

It’s important to ensure that you have enough data in each score bin. Each of the six score bins we created in the table above contains at least 10% of the development sample data. In a perfect world, we would have 16.7% of the data (100 divided by 6 score range bins) in each bin.

Now we can apply these score range bins to our monitoring sample to see how the distribution of data within each bin compares across the two samples.

# Capture the score range bins from the development sample as a vector that can be 
# passed to `cut()`, so that we can apply the same bin breaks to the monitoring
# sample
points_cuts <- gregexpr(
  pattern = "[0-9]+",
  text = as.character(development_score_ranges$bin)
)

points_cuts <- regmatches(
  x = as.character(development_score_ranges$bin),
  m = points_cuts
) |> 
  unlist() |> 
  unique()

# Apply the score range bins to the monitoring sample
monitoring_sample <- monitoring_sample |> 
  dplyr::mutate(
    bin = cut(
      points,
      breaks = points_cuts,
      right = TRUE, 
      include.lowest = TRUE
    )
  )

monitoring_score_ranges <- monitoring_sample |> 
  dplyr::count(bin) |> 
  dplyr::mutate(prop = n / sum(n))

# Create a summarized table, grouped by score range bin, that can be compared to the
# development sample
monitoring_score_ranges |> 
  dplyr::mutate(prop = scales::percent(prop)) |> 
  knitr::kable(
    col.names = c(
      "Score Range Bin", 
      "# of Cases in Monitoring Sample", 
      "% of Monitoring Sample"
    ), 
    align = c("l", "r", "r"),
    caption = "Score Range Bins (Applied to Monitoring Sample)"
  )

Score Range Bins (Applied to Monitoring Sample)
Score Range Bin	# of Cases in Monitoring Sample	% of Monitoring Sample
[188,215]	29	14.5%
(215,221]	24	12.0%
(221,227]	30	15.0%
(227,237]	35	17.5%
(237,241]	29	14.5%
(241,274]	53	26.5%

Now we can compare the distribution of the data in each score range bin between the development and monitoring samples:

# Join the monitoring summary table to the development summary
comparison_table <- development_score_ranges |> 
  dplyr::left_join(
    monitoring_score_ranges,
    by = "bin",
    suffix = c("_development", "_monitoring")
  )

# Show the comparison table
comparison_table |> 
  dplyr::select(-(dplyr::starts_with("n_"))) |> 
  dplyr::mutate(
    dplyr::across(
      .cols = -bin,
      .fns = scales::percent
    )
  ) |> 
  knitr::kable(
    col.names = c(
      "Score Range Bin", 
      "% of Development Sample",
      "% of Monitoring Sample"
    ), 
    align = c("l", "r", "r"),
    caption = "Comparison of Score Range Distributions"
  )

Comparison of Score Range Distributions
Score Range Bin	% of Development Sample	% of Monitoring Sample
[188,215]	19.2%	14.5%
(215,221]	14.2%	12.0%
(221,227]	19.4%	15.0%
(227,237]	15.3%	17.5%
(237,241]	16.6%	14.5%
(241,274]	15.3%	26.5%

You may prefer to visualize this same comparison data in a chart, as opposed to a table:

comparison_table |> 
  dplyr::select(-(dplyr::starts_with("n_"))) |> 
  # Convert data to long format
  tidyr::pivot_longer(
    cols = -bin,
    names_to = "prop_sample",
    values_to = "value"
  ) |> 
  # Improve labels
  dplyr::mutate(
    prop_sample = dplyr::case_when(
      prop_sample == "prop_development" ~ "Development",
      prop_sample == "prop_monitoring" ~ "Monitoring",
    )
  ) |> 
  ggplot2::ggplot() +
  ggplot2::geom_bar(
    mapping = ggplot2::aes(
      x = prop_sample, 
      y = value, 
      fill = bin
    ),
    stat = "identity",
    color = "black",
    position = ggplot2::position_fill(reverse = TRUE)
  ) +
  ggplot2::scale_y_continuous(labels = scales::label_percent()) +
  ggplot2::coord_flip() +
  ggplot2::scale_fill_brewer(
    name = "Score Range Bin", 
    palette = "RdYlGn", 
    direction = 1
  ) +
  ggplot2::labs(
    title = "Comparison of Score Range Distributions",
    x = "Sample",
    y = "Distribution of Sample"
  ) +
  ggplot2::theme_bw()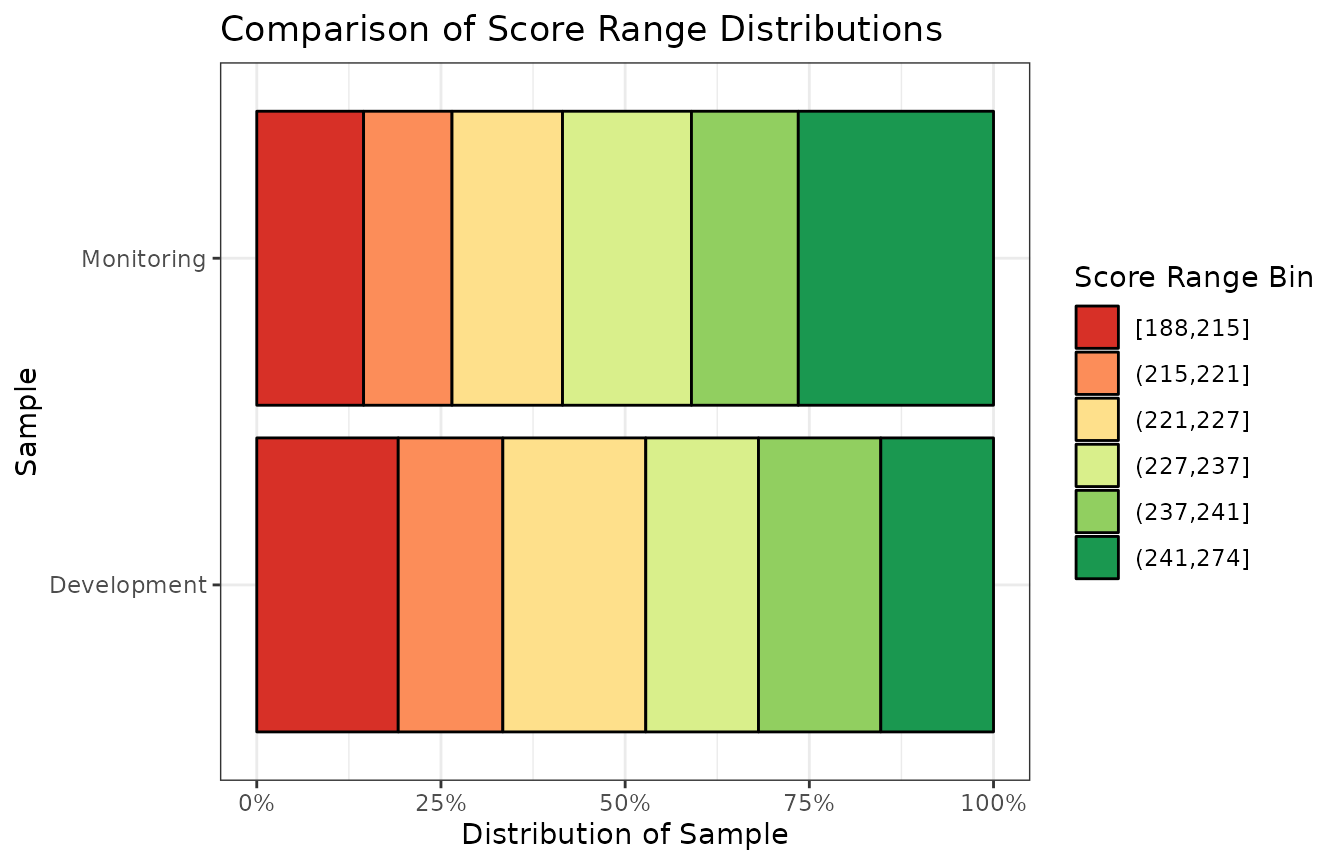

Population Stability Index

Once we have our development and monitoring data summarized by score ranges, we can compute the Population Stability Index via the formula below:

\[ \sum \Bigg[ \Big( \text{% Monitoring}_{b} - \text{% Development}_{b} \Big) * ln \Bigg( \frac{ \text{% Monitoring}_{b}}{ \text{% Development}_{b}} \Bigg) \Bigg] \] for each unique score range bin $b$.

The index can be interpreted as follows:

A value less than 0.1 shows no significant change
A value between 0.1 and 0.25 denotes a small change that needs to be investigated
A value greater than 0.25 points to a significant shift in the applicant population

We can use the psi() function from {KAscore} to compute the population stability index value for the monitoring sample:

# Compute the Population Stability Index
population_stability_index <- psi(
  x = development_sample$bin,
  y = monitoring_sample$bin
)

The population stability index value is 0.1, which indicates that there is a small change that needs to be investigated. In the comparison table, we see that the percentage of monitoring cases in the (241, 274] score range bin is higher than in the development sample. We can also see that the percentage of monitoring cases in the [188, 215] score range bin is lower than in the development sample. This indicates that our applicant pool is actually scoring better (i.e., higher) than the applicant pool used to develop the model.

Chi Squared Goodness of Fit Test

We can also perform a Chi-Squared Goodness of Fit Test as another way to determine if the two samples’ score range distributions are statistically different. The null hypothesis of this test is that the two samples being compared were drawn from the same population (i.e., the applicant pool within the monitoring sample behaves similarly to the applicant pool within the development sample). A small p-value (e.g., less than 0.05) would cause us to reject the null hypothesis, and lead us to believe that the monitoring sample is showing a shift in the applicant pool being scored by our model.

# Compute the Chi-Squared test
chi_sq <- rbind(
  comparison_table$n_development, 
  comparison_table$n_monitoring
) |> 
  as.table() |> 
  chisq.test()

# Show the test results
chi_sq
#> 
#>  Pearson's Chi-squared test
#> 
#> data:  as.table(rbind(comparison_table$n_development, comparison_table$n_monitoring))
#> X-squared = 17.457, df = 5, p-value = 0.00371

We see that the p-value is 0.004. If we are using a significance threshold of 0.05, this would mean that the applicant pool within the monitoring sample behaves differently than the applicant pool that was used to develop the model. This result would imply that a change to the model should be explored (e.g., consider replacing and/or adding independent variables, re-training the model using data from a window closer to present, weight newer cases in the training data heavier than older cases).

Characteristic Analysis Index

Shifts in the distributions of the scores can only be caused by the independent variables in the scorecard. While the population stability index details shifts in the population at the level of the overall model, the characteristic analysis index similarly details shifts in the population within each independent variable.

The characteristic analysis index is computed as follows:

\[ \sum \Big( \text{% Monitoring}_{c} - \text{% Development}_{c} \Big) * \text{Points}_{c} \]

for each unique level $c$ in the independent variable being analyzed.

Let’s take a look at an example of a characteristic analysis for the Industry independent variable, using the cai() function from {KAscore}.

# Select rows of interest from our card
card_industry_points <- card |> 
  dplyr::filter(variable == "industry") |> 
  dplyr::select(-variable)

# Perform the analysis
characteristic_analysis <- cai(
  data = card_industry_points,
  x = development_sample$industry,
  y = monitoring_sample$industry,
  verbose = FALSE
)

# Show the characteristic analysis table
characteristic_analysis$classes |> 
  dplyr::mutate(
    dplyr::across(
      .cols = dplyr::starts_with("prop_"),
      .fns = scales::percent
    )
  ) |> 
  knitr::kable(
    col.names = c(
      "Industry", 
      "% of Development Sample", 
      "% of Monitoring Sample", 
      "Points",
      "CAI"
    ),
    align = c("l", "r", "r", "r", "r"),
    caption = "Characteristic Analysis Index - Industry"
  )

Characteristic Analysis Index - Industry
Industry	% of Development Sample	% of Monitoring Sample	Points	CAI
	0.9%	0.5%	110	-0.440
beef	9.7%	10.5%	69	0.552
dairy	18.1%	15.0%	73	-2.263
fruit	23.4%	19.0%	65	-2.860
grain	28.0%	25.0%	87	-2.610
greenhouse	1.2%	0.5%	61	-0.427
nuts	2.2%	1.5%	67	-0.469
pork	5.0%	4.0%	58	-0.580
poultry	10.3%	22.5%	97	11.834
sod	1.2%	1.5%	71	0.213

Looking at the individual values in the table above, we can see that the new loan applicant pool (the monitoring sample) are shifting towards more poultry loans, and moving slightly away from almost all of the other industries.

The total characteristic analysis index value for Industry, which can be accessed through characteristic_analysis$net, is equal to 3. In other words, within the industry independent variable, new loan applicants (in the monitoring sample) are scoring 3 points higher than the applicant pool in the development sample. This may lead us to investigate what led to the increase in poultry loan applications last month (marketing campaign, seasonality, etc.).

To complete the characteristic analysis index for our model, we could repeat this exercise for the other independent variables in our model (Housing Status and Collateral Type).

Comparing Multiple Monitoring Windows

The analysis performed so far indicates that there are differences in the score distributions between development sample and applicants who were scored by the model last month (i.e., the monitoring sample). As you collect more data for monitoring purposes, it can be useful to create multiple monitoring “windows” for analysis. For example, creating monitoring samples of data from the past month, three months prior, six months prior, etc., can help detect any emerging trends or confirm that any deviations in one particular month do not represent longer-term trends.

Let’s complement our analysis with data corresponding to applicants from three (three_months_ago_sample) and six (six_months_ago_sample) months ago.

We can use the following code to compute the score range distributions:

# Simulate a monitoring sample from 6 months ago
six_months_ago_sample <- loans |> 
  dplyr::select(industry, housing_status, collateral_type) |> 
  dplyr::sample_n(size = 250) |>
  dplyr::mutate(loan_id = dplyr::row_number() + 200000)

# Simulate a monitoring sample from 3 months ago
three_months_ago_sample <- loans |> 
  dplyr::select(industry, housing_status, collateral_type) |> 
  dplyr::sample_n(size = 300) |>
  dplyr::mutate(loan_id = dplyr::row_number() + 400000)

# Add the score range bins and points to the monitoring sample from 6 months ago
six_months_ago_score_ranges <- six_months_ago_sample |>
  tidyr::pivot_longer(
    cols = -loan_id, 
    names_to = "variable", 
    values_to = "class"
  ) |>
  dplyr::left_join(card, by = c("variable", "class")) |> 
  dplyr::summarise(
    points = sum(points), 
    .by = loan_id
  ) |> 
  dplyr::mutate(
    bin = cut(
      points,
      breaks = points_cuts,
      right = TRUE, 
      include.lowest = TRUE
    )
  ) |> 
  dplyr::count(bin) |> 
  dplyr::mutate(prop = n / sum(n)) |> 
  dplyr::select(-n)

# Add the score range bins and points to the monitoring sample from 6 months ago
three_months_ago_score_ranges <- three_months_ago_sample |>
  tidyr::pivot_longer(
    cols = -loan_id, 
    names_to = "variable", 
    values_to = "class"
  ) |>
  dplyr::left_join(card, by = c("variable", "class")) |> 
  dplyr::summarise(
    points = sum(points), 
    .by = loan_id
  ) |> 
  dplyr::mutate(
    bin = cut(
      points,
      breaks = points_cuts,
      right = TRUE, 
      include.lowest = TRUE
    )
  ) |> 
  dplyr::count(bin) |> 
  dplyr::mutate(prop = n / sum(n)) |> 
  dplyr::select(-n)

We can compare the score distribution of development sample and the monitoring samples for several historical periods with the following code:

dplyr::bind_rows(
  # Development sample
  development_score_ranges |> 
    dplyr::select(-n) |> 
    dplyr::mutate(sample = "Development"),
  # Last month's monitoring sample
  monitoring_score_ranges |> 
    dplyr::select(-n) |> 
    dplyr::mutate(sample = "Monitoring (Last Month)"),
  # Monitoring sample from 3 months ago
  three_months_ago_score_ranges |> 
    dplyr::mutate(sample = "Monitoring (3 Months Ago)"),
  # Monitoring sample from 6 months ago
  six_months_ago_score_ranges |> 
    dplyr::mutate(sample = "Monitoring (6 Months Ago)")
) |> 
  ggplot2::ggplot(
    mapping = ggplot2::aes(
      x = bin,
      y = prop,
      group = sample,
      color = sample
    )
  ) +
  ggplot2::geom_line() +
  ggplot2::geom_point() +
  ggplot2::scale_y_continuous(labels = scales::label_percent()) +
  ggplot2::labs(
    title = "Popluation Stability Chart",
    subtitle = "Across multiple monitoring windows",
    x = "Score Range",
    y = "Distribution of Sample",
    color = NULL # Remove legend title
  ) +
  ggplot2::theme_bw()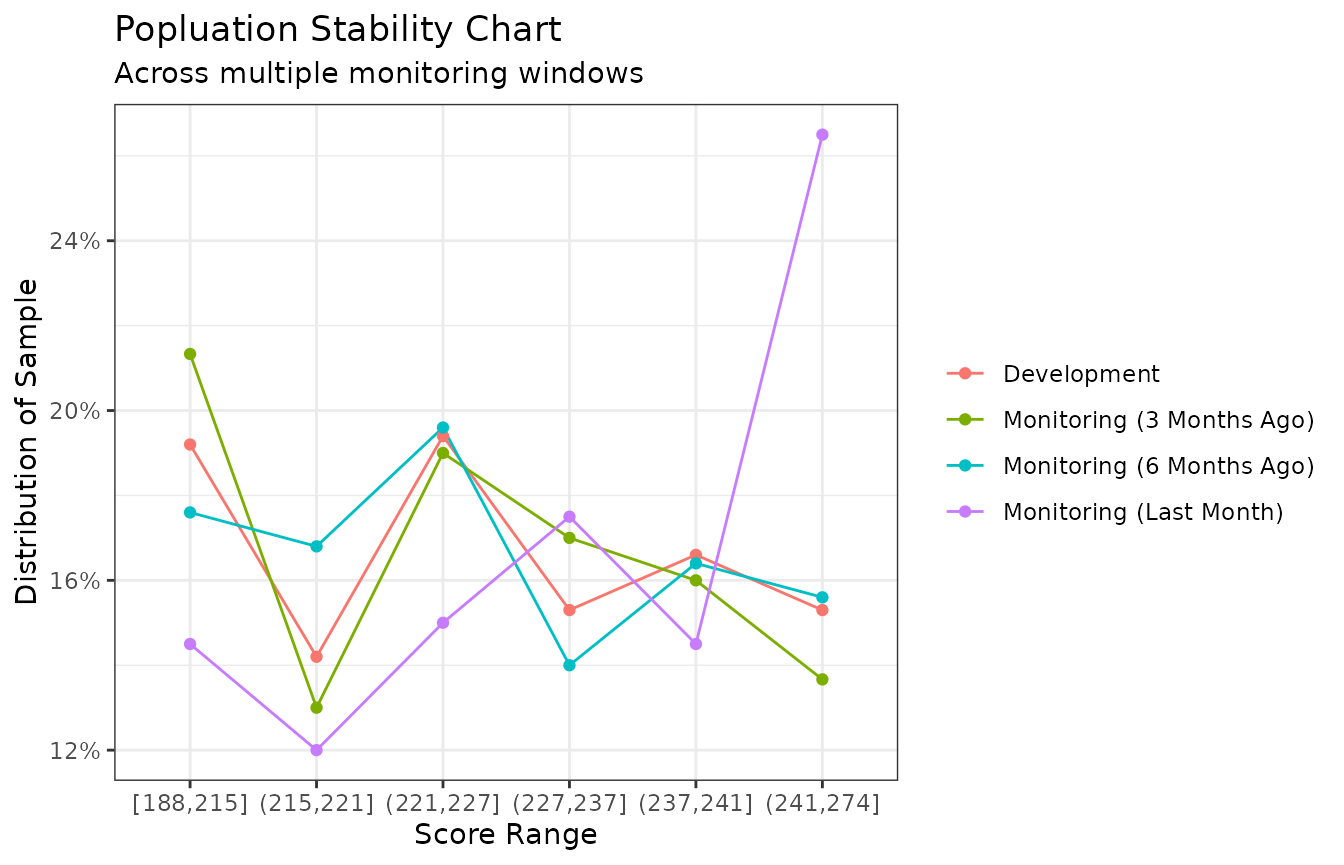

We see that applicants from last month show a deviation from the loan applicant pool used during development, especially in the highest score range bin, (241, 274]. However, the next most recent monitoring sample (from 3 months ago) shows a distribution much closer to the development sample across all score range bins. This tells us that the differences between last month’s monitoring sample and the development sample may be due to random noise, as opposed to any trend taking place that would indicate a shifting population.

If, instead, distributions for the monitoring samples from three and six months ago also showed deviations similar to the monitoring sample from last month, we would conclude that the trend started more than six months ago and we may want to consider re-training the scorecard.

Additional Considerations

The population stability index, Chi-Squared test, and characteristic analysis index should all be taken into consideration alongside subject matter expertise. Understanding economic trends that affect your loan applicant pool can provide the context necessary to make decisions on whether or not to alter your scorecard model. It’s important to consider what information outside of your scorecard (i.e., information that is not represented in the independent variables of your model) may be having an impact on its performance since it was developed.

While the population stability index, Chi-Squared test, and characteristic analysis index statistics focus on the current schema of the model in production, it is good practice to continue to monitor other attributes that were considered to be independent variables during development, but were not incorporated in the production model due to weak signal. As you continue to gather more performance data over time, the information value statistic (via the iv() function from the {KAscore} package) for each of these unused attributes should be re-computed periodically to assess if they should be incorporated into the model to boost predictive accuracy. Conversely, the information value for each independent variable in the production model should also be periodically re-computed to ensure it is not decreasing the model’s predictive accuracy.

In the event that a significant shift in the loan applicant population has taken place since the model was developed, the most important first step is to work with domain experts to try to identify or hypothesize what caused the shift. If possible, engineer one or more features (i.e., potential independent variables) using this hypothesis and relevant available data, develop a “competitor” scorecard model using these new independent variable(s) (and removing any that are hindering the production model’s ability to recognize the shift taking place), and compare the competitor model’s accuracy to the production model’s accuracy using a held-out test sample that encompasses a more recent population than what was used to train the current model in production.